Currents

Mathematical models answer farmers’ questions about infectious disease

David Elzinga has a history of using math to help animals survive. From moose suffering from too many ticks to bats with fungal infections, Elzinga has developed mathematical models to answer a plethora of questions biologists have about the spread of disease. 

Elzinga, a UW-La Crosse assistant professor of Mathematics & Statistics, recently presented “Baa-ttling Sore Mouth in Sheep” at a symposium in Richmond, Virginia. Sore Mouth, a viral infection primarily of sheep and goats, is a global problem that has been the most destructive in developing countries that depend on healthy flocks for their livelihood, as well as major sheep producers in the U.K. and Australia. Although sore mouth is not a major management concern in the U.S., Elzinga is finding new ways to use mathematical models help Midwestern farmers analyze the health of their flocks.  

The beauty of mathematical models is that no costly or inhumane testing is involved — like slaughtering half a flock of sheep to test out one control method. Elzinga compares mathematical modeling to building a paper airplane to see how modifications to a real plane would work. You can bend a wing to evaluate flight changes without the risk of crashing a real plane.  

“We want to transform what we see in the real world into a simplified computer reality,” explains Elzinga.  “Like a computer game, with my mathematical model, I can see what happens as we change variables — all within the model on the computer.” 

Elzinga uses differential equations from calculus in the mathematical models to analyze how adaptations could potentially protect sheep health — like increasing the rate of vaccination or isolating a group of sheep. The ideas he applies to the models are aligned with questions from government, wildlife organizations and even vaccine development companies.  

Elzinga isn’t the only one applying mathematics to help solve biology questions on the UWL campus. A MathBio Working Group at UWL has been meeting regularly for more than a decade to help solve problems at the intersection of math and biology. Initially a student and faculty group, in 2014 scientists from both the US Geological Survey (USGS) and the US Fish and Wildlife Service (USFWS) joined.  

Since 2018, James Peirce, professor of Mathematics & Statistics, and Greg Sandland, professor of biology, have been working with USGS to develop mathematical models to help with the problem of invasive carp in the Illinois and Mississippi Rivers. This work has now expanded to include the entire MathBio Working Group, along with a number of undergraduate research students.   

“Our hope is that these models will help to guide management strategies aimed at reducing carp numbers in these systems,” says Sandland.  

Solutions for sheep farmers

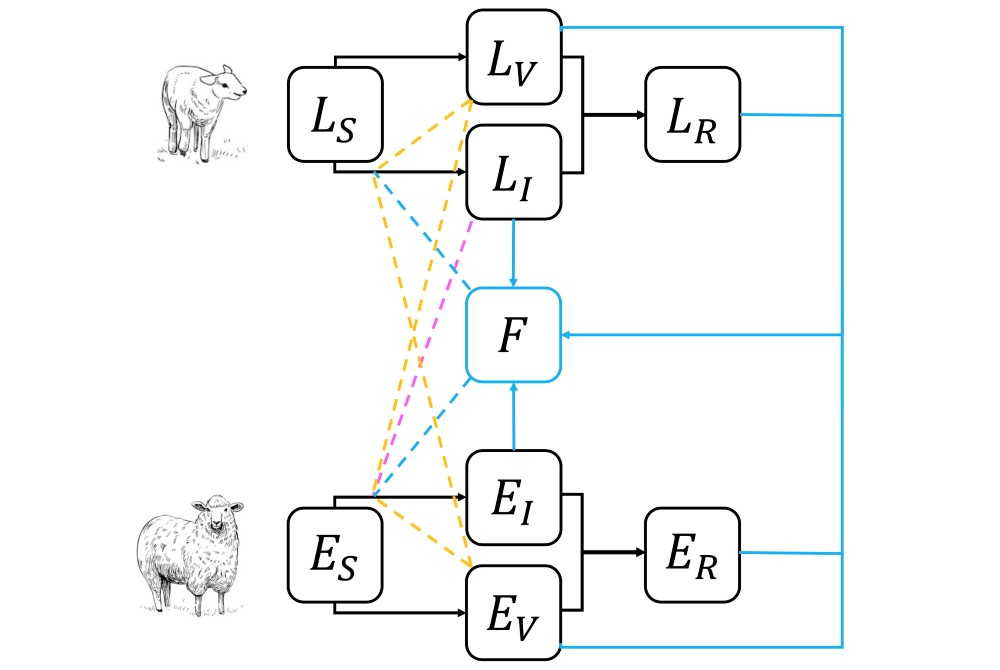
Elzinga’s sore mouth sheep models have provided some answers for farmers about control strategies and more. The results will be published this spring in an international veterinarian journal and shared with various organizations such as UW Extension to help spread the word among farmers. Among the results Elzinga found that: 

• Regular monitoring of disease and isolating sheep has a much better potential to prevent outbreaks on a small farm than on a large one. For a large farms with 100s or thousands of sheep, farmers would need to isolate more than 99 % of the sick sheep immediately to stop the spread — an unreal expectation. But the picture looked brighter for small farms with herds of up to 100 sheep as farmers would have a period of 2-3 weeks to find the sick sheep and isolate them. This suggests that regular monitoring for outbreaks followed by isolation is only a realistic management plan for small flocks, whereas large flocks must rely on intensive biosecurity measures to prevent sick sheep from being introduced into the flock. 
• If one new sick sheep was introduced to the herd, it would spread to about 12 other sheep. Those 12 would spread to another 12 sheep and so on. At this rate it’s easy to see how a disease outbreak would spread quickly in a large herd of hundreds or thousands of sheep, yet how it would be easier to monitor in smaller herds. 
• Fomites, spots in the environment that harbor viruses like feeding troughs, can ignite an outbreak on sheep farms. His models show an area around a trough erupting in cases after just a few sheep were previously sick.  

Elzinga says a big push in the mathematical modeling community right now is to get closer to stakeholders. For his next project, he has been working directly with a sheep farm in Ottawa, Illinois and will base his model off a map of their real farm and animals. Using this specific data, he can let the farmer know answers to questions that could potentially save money and improve sheep health.  

Elzinga’s work is all about applying math. While math sometimes gets a bad rap for being highly theoretical, Elzinga says it’s because schools teach numerous, individual math tools early in the curriculum and few students get to the point in education where they see how those tools work together on real world problems. 

“How many times do you get to see applications in school before you’re done with math?” asks Elzinga. “Someone has shown them the hammer, the screwdriver and the ruler, but no one said, ‘with these tools you can build a bookshelf.’” 

What is mathematical modeling?

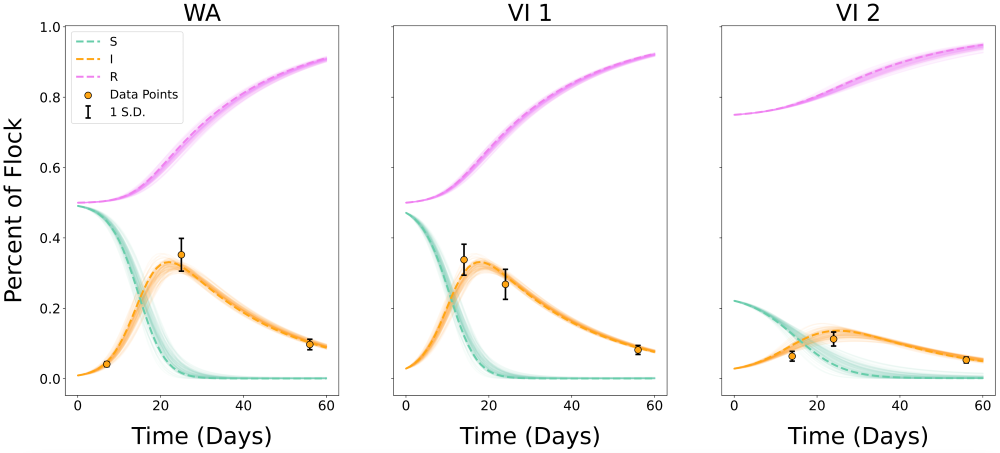
Mathematical models are basically a simplified form of something happening in the real world – like how paper airplanes are models of real airplanes. With a model, you can try out things you wouldn’t want to do in real life, like changing the shape of a wing to test how a real plane flies with the modification. One of the first steps of mathematical modeling is getting your math to replicate reality, which means finding specific facts that are already known and producing those with the model. Then, mathematicians can move on to the unknown – changing the variables and analyzing how the model responds.